CORDIC Accelerator 2: Coordinate transforms
Consider this setup:
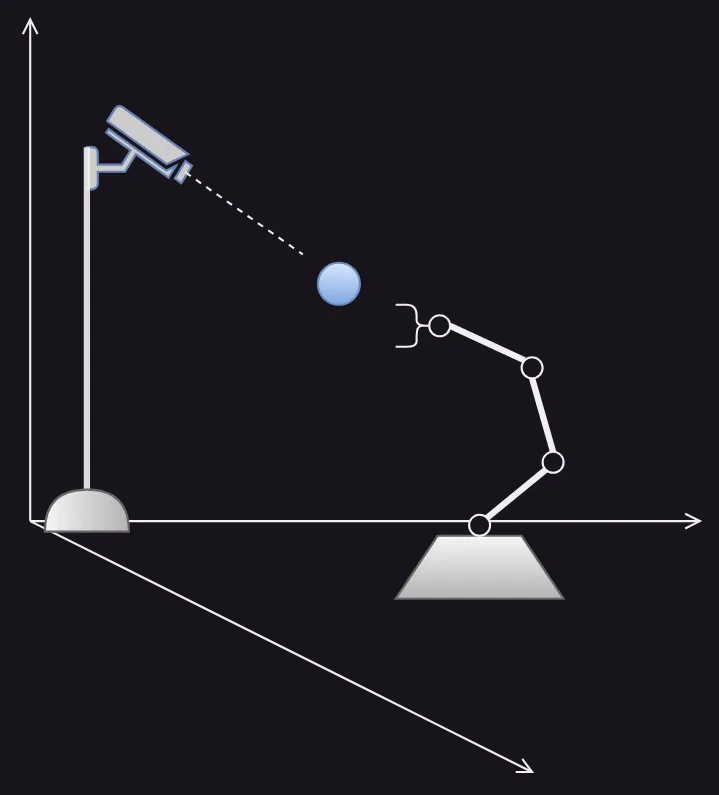
A depth camera mounted on a stand looks at a ball in 3D space. The 4 DoF robotic arm wishes to grab the ball.
The depth camera knows where the ball is located in terms of (horizontal distance from left side of frame), (vertical distance from bottom of frame), and (distance from camera).
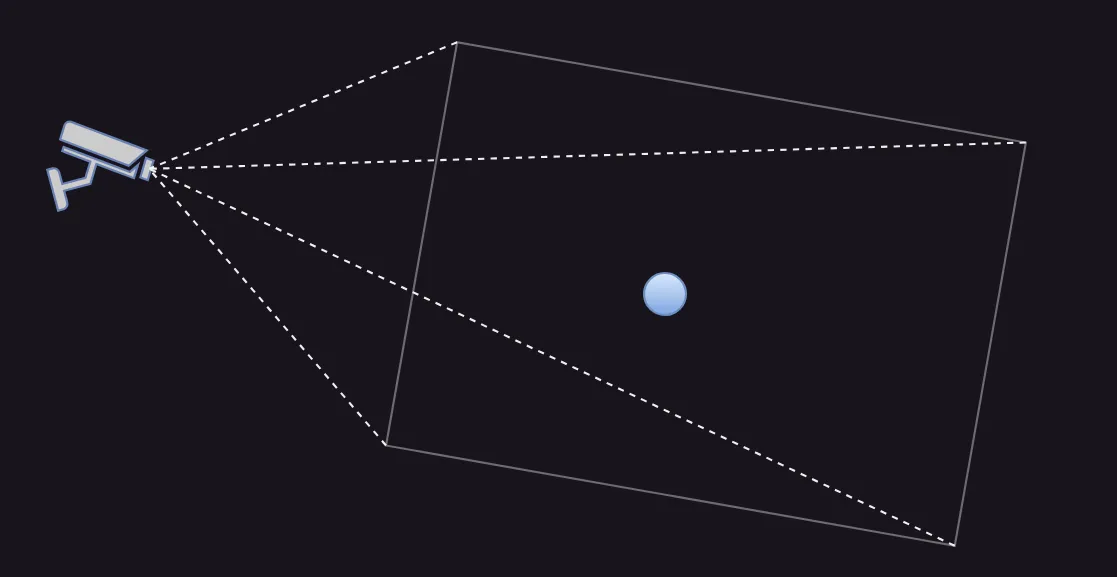
The system at hand can transform this position in terms of the camera's frame to position in terms of the global frame (3D Euclidean space). Using the camera's rotation (for instance tilt angle), and translation from the axes (due to the stand) we construct its pose matrix, and calculate the vector product of this 4x4 matrix with the position of the ball in camera frame.
The product is the position of the ball in the global frame.
The camera + stand are made up of one link (the stand) and one joint (the camera's axis of rotation). The robotic arm is comprised of four links (its base + the three arm segments) and four joints of rotation.
By vector multiplying the sequential pose matrices of each of the arm's links and joints, we can get the position of the end effector in terms of global coordinates, just like we did for the camera.